题目
源地址:
http://poj.org/problem?id=2714
理解
一开始以为只是一道简单的求解最远距离的题目,但是敲完代码之后发现前两个样例过了,最后一个样例数据差距很大。然后仔细读题才发现,题目中给定的正负是不定的= =。一时间没有思路,以为需要使用DP的思想,然后去看了discuss,才明白用枚举的方法列出每一个向量,减少了很大的复杂度,使得问题能在1s之内解决。
新技能get
位运算
下面列出一张简表
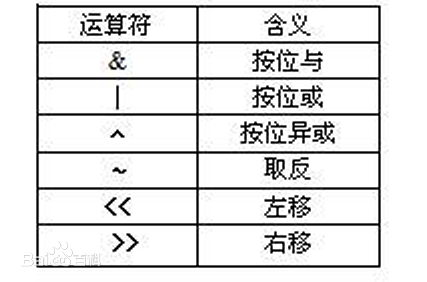 注意区分位运算
注意区分位运算~与逻辑运算!的区别。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int N = 105;
double mx, my, cx, cy;
struct V
{
double x, y;
bool operator < (const V &a) const
{
double t = atan2(y, x);
double at = atan2(a.y, a.x);
return t < at;
}
} v[N << 1];
int main(int argc, char const *argv[])
{
int n, i, ci, end;
double x, y;
while (~scanf("%d", &n) && n)
{
for (i = 0; i < n; i++)
{
scanf("%lf%lf", &x, &y);
v[i << 1].x = x;
v[i << 1].y = y;
v[i << 1 | 1].x = -x;
v[i << 1 | 1].y = -y;
}
sort(v, v + (n << 1));
cx = cy = 0;
for (i = 0; i < n; i++)
{
cx += v[i].x;
cy += v[i].y;
}
mx = cx; my = cy;
for (i = 0, end = n << 1; i < end; i++)
{
ci = (i + n) % end;
cx += v[ci].x - v[i].x;
cy += v[ci].y - v[i].y;
if (cx * cx + cy * cy > mx * mx + my * my)
mx = cx, my = cy;
}
printf("Maximum distance = %.3f meters.\n", sqrt((double)mx * mx + my * my));
}
return 0;
}
更新日志
- 2014年07月15日 已AC。