I recently came across an insightful article on SQL Query Optimizers by @leiysky on Zhihu, and I must say it was excellent! To make it accessible to a wider audience, I have translated the piece into English. Enjoy reading!
Please note that @leiysky deserves full credit for the quality of this article. Any mistakes are solely due to my inadequate translation skills.
Alright, let's begin!
During our recent conversation, Mr. Chi and I discussed his latest project at CMU called optd, which is a query optimizer library developed using the Cascades framework. We ended up griping together about various design and implementation aspects of database optimizers. It was at that moment when I realized the intriguing nature of certain technical subjects and decided to take note of them.
So, I've made the decision to launch a series where we'll cover everything about query optimizers—ranging from algorithm basics to engineering techniques, technological evolution to project implementation, and even some insider industry gossip.
The inspiration of the title comes from Haruki Murakami's book, which I highly recommend. The book is a collection of essays that Murakami wrote about his experience as a runner. The title is a reference to a collection of short stories by Raymond Carver, "What We Talk About When We Talk About Love", which Murakami translated into Japanese.
Software development is a skill just as running is, everyone can do it by practising but not everyone will have the same feelings about it. I'd like to share some personal thoughts and experiences about query optimizers, and I hope that you will find them interesting.
Today, let's begin by discussing the topic of IR Design, focusing on common design patterns in optimizers and the underlying considerations.
What is a Query Optimizer?
Before we officially start the discussion, I'd like to clarify the definition of a query optimizer.
In general, a query optimizer is a database component that optimizes the execution plan of queries. However, different databases have various methods for optimizing queries. For instance, some may directly rewrite the AST, perform transformations during AST lowering, or dynamically rewrite during query execution.
To unify the concept, I will refer to all parts from the SQL parser to the SQL Executor collectively as the Query Optimizer.
What is IR?
Friends familiar with compilation technology should be very familiar with the term IR. IR stands for Intermediate Representation, which is commonly used in compilers for different programming languages like Rust's HIR & MIR and LLVM's LLVM IR. IR serves as a structural representation of programming languages, enabling the compiler to conduct various analyses and optimizations more effectively.
If SQL is considered a programming language, then relational databases function as virtual machines that execute SQL, similar to how the JVM executes Java. The query optimizer is responsible for translating SQL statements (Java code) into execution plans (Java bytecode) for the executor (Java runtime) to execute. Consequently, it is essential to design different IRs for SQL when developing a query optimizer.
What does SQL IR look like?
Typical database projects are divided into several modules: Parser, Analyzer/Binder, Optimizer, and Executor. These components process SQL statements sequentially to transform them into query results. In our context, the Optimizer includes both the Analyzer and Optimizer modules mentioned earlier.
AST
SQL is a declarative language that mimics natural language syntax. It is based on relational algebra and can describe operations on sets, mapping them to queries on tabular data (tables).
To facilitate processing, like the vast majority of compilers, we will first parse SQL language into an AST (Abstract Syntax Tree). A typical SQL AST is illustrated as follows:
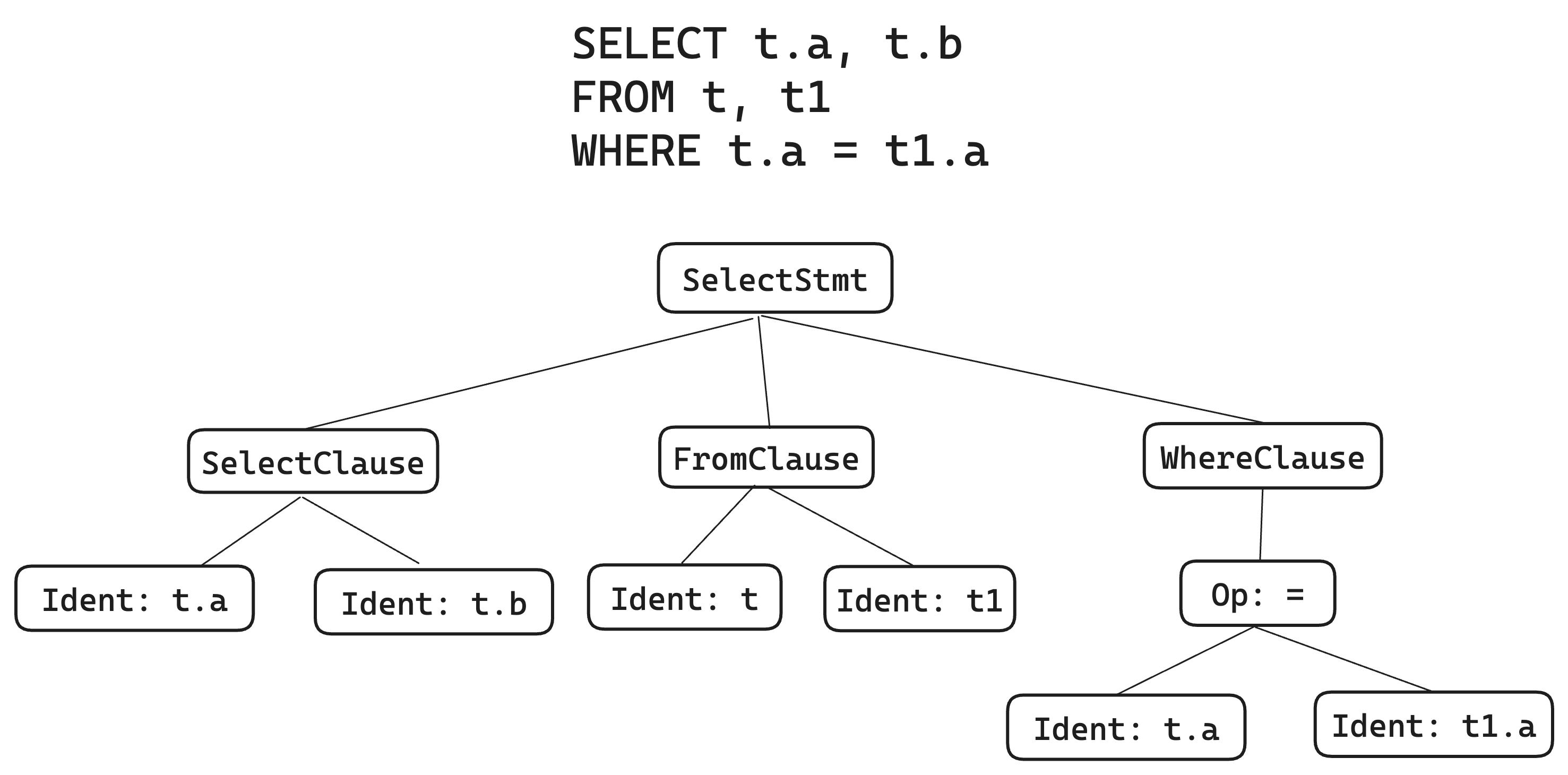
In the SQL AST, we generally divide nodes into two types: Statement (Stmt) and Expression (Expr). The root node of each SQL AST is always a Statement, which may contain some Clauses as well as Expressions. An Expression is a recursive structure that includes various operators and function calls, and even nested Statements (Subqueries).
One interesting aspect of SQL is the blurred boundary between Statements and Expressions in SELECT Statements. This occurs because SELECT Statements are recursive and must address operator precedence issues (UNION/EXCEPT/INTERSECT). Additionally, only SELECT Statements can interact with Expressions recursively, which should be considered when designing an SQL AST.
Relational Algebra
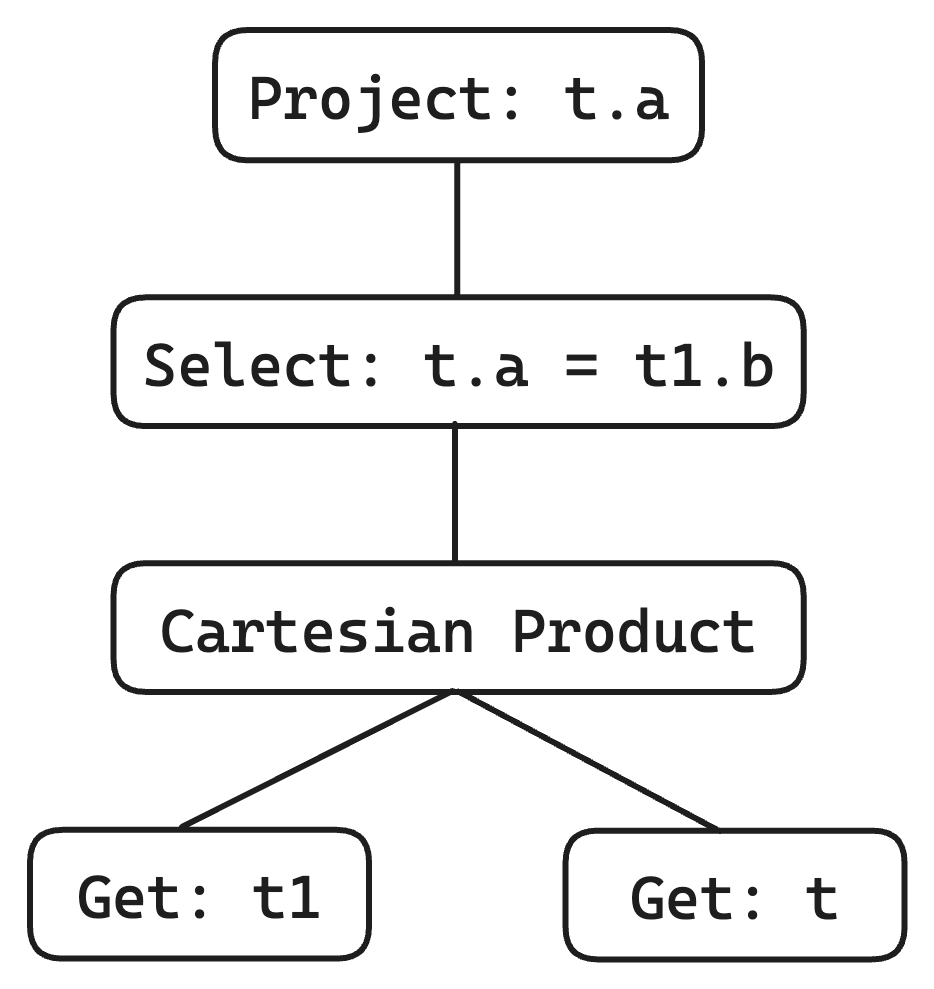
The theoretical foundation of the SQL language is relational algebra, and every query statement corresponds to a representation in relational algebra. For example:

Since the expression of relational algebra is also a recursive tree structure, many systems naturally convert SQL AST into an execution plan similar to the one shown below. We refer to each node as an operator, and we call the entire operator tree a query plan.
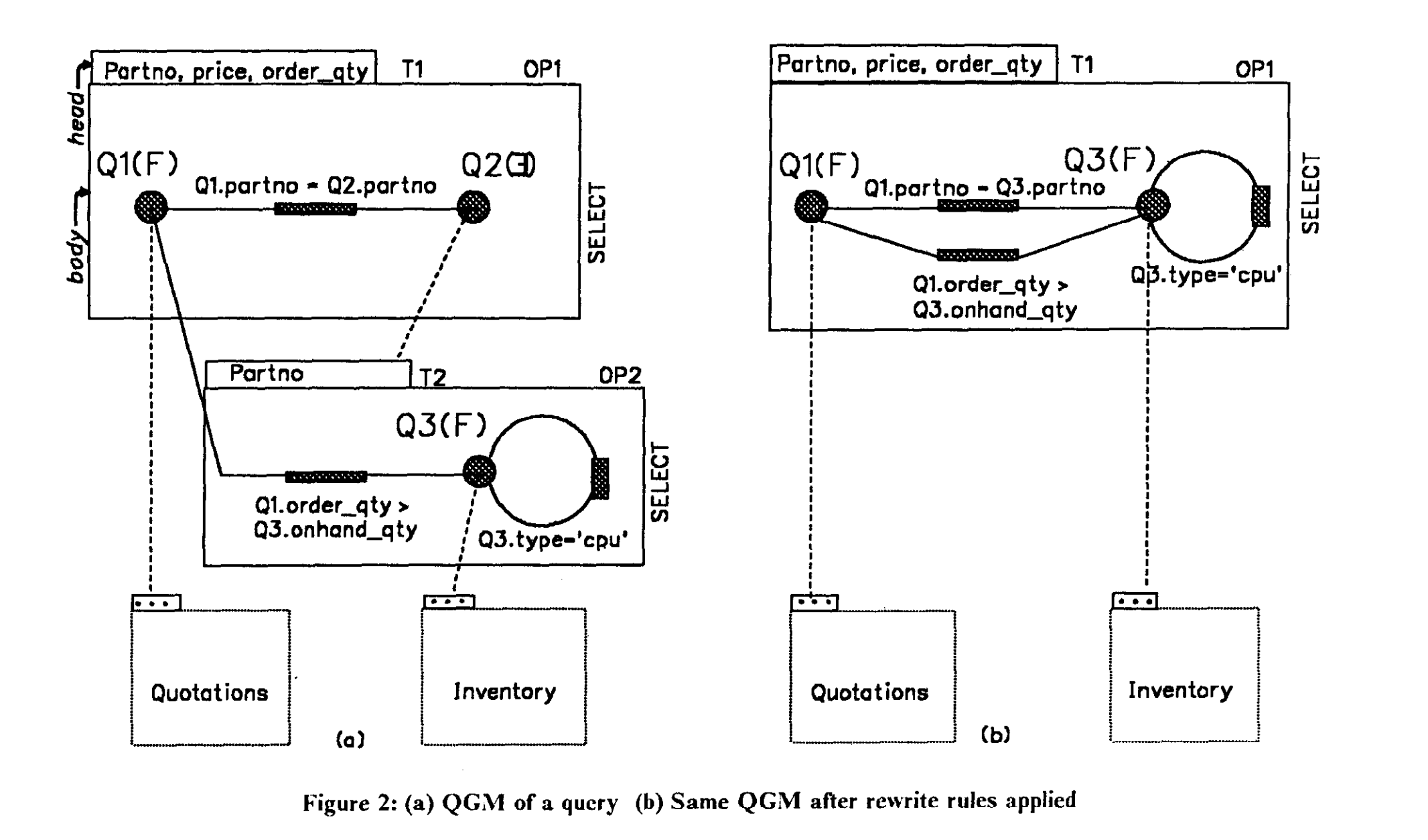
Of course, there are exceptions among the many systems. For example, IBM, as a pioneering, introduced the Query Graph Model (QGM) in its Starburst system. This representation is quite abstract and hardcodes many properties into QGM, making it exceptionally difficult to understand. Its claimed extensibility is also questionable.
Due to space limitations, I won't elaborate here; if interested, you can read the related papers Extensible Query Processing in Starburst and Extensible/Rule Based Query Rewrite Optimization in Starburst.
Currently, mainstream databases have essentially adopted the representation of relational algebra (such as IBM's System R and DB2, Oracle's various database products, Microsoft's SQL Server series, open-source PostgreSQL and MySQL 8.0). Based on this foundation, they have developed numerous optimization frameworks and execution frameworks. Therefore, choosing to use the abstraction of relational algebra when designing SQL IR is a foolproof decision.
By utilizing the various axioms and theorems of relational algebra, we can perform a variety of transformations on SQL IR to achieve optimization while ensuring correctness. Specific optimization rules and algorithms will be discussed in subsequent articles.
(My) Best Engineering Practices
There is a cognitive bias known as the curse of knowledge, which occurs when one assumes that others possess the same level of knowledge during communication.
This phenomenon is quite common in software development. People who have experience writing certain types of code and those who don't often struggle to communicate effectively, even if they share the same theoretical foundation (algorithms, programming languages, or domain knowledge). The reason for this lies in the significant flexibility of software engineering; there are multiple ways to implement the same functionality, each with its own set of challenges.
To eliminate such communication barriers, various technical fields have developed their own set of idioms or design patterns. New projects built on these practices can avoid a lot of unnecessary trouble. The same is true for the field of databases; however, due to its niche nature and high degree of commercialization, knowledge circulated among the public is very scarce, and engineering practices are scattered across various open-source projects.
In this article, I will build a SQL IR from scratch based on my own best practices, which will facilitate the progressive sharing of some design considerations. Due to personal preference, I will use Rust to write code. Friends who are not familiar with Rust need not worry; as long as you have a basic understanding of C/C++, you can comprehend the logic behind Rust's code.
Hello, world!
When we learn a new programming language, the first program we generally encounter is "hello world".
fn main() {
println!("Hello, world!");
}Therefore, we will also start by building our IR from the SQL version of "hello world".
create table t(a int);
select * from t;Translating this SQL statement into relational algebra is very straightforward; we denote it as Get(t), which means to return all the data in set t. To represent such a query, we can define a simple struct called Get.
pub struct Get {
pub table: String,
}
fn plan() -> Get {
// select * from t;
Get {
table: "t".to_string(),
}
}This simple SQL IR is now complete. With the Get, we can represent all queries similar to select * from xxx. Isn't it very straightforward?
Select & Project
Next, we can add more features to this IR, supporting additional SQL clauses. For example:
create table t(a int, b int);
select a from t where a = 1;This SQL query, when translated into relational algebra, can be denoted as Project(Select(Get(t), a = 1), a). The Select operator can filter data based on the provided predicate, while the Project operator can trim the set to obtain the required attribute. To represent such a query, we need to add more struct definitions.
pub struct Get {
pub table: String,
}
pub struct Select {
pub get: Get,
pub predicate: String,
}
pub struct Project {
pub select: Select,
pub project: String,
}
fn plan() -> Project {
// select a from t where a = 1;
Project {
select: Select {
get: Get {
table: "t".to_string(),
},
predicate: "a = 1".to_string(),
},
project: "a".to_string(),
}
}Upon arriving here, we are confronted with several questions: According to the theorem of relational algebra, can Project act as a child of Select? Given that Select is optional for an SQL query, how should this be reflected in the code?
To address these issues, we can introduce some features of dynamic dispatch. In C++/Java, inheritance is commonly used to represent an Operator, for example:
class Operator {};
class Get : public Operator {};
class Select : public Operator {
Operator* _child;
};
class Project : public Operator {
Operator* _child;
};In Rust, we have a more convenient option that allows us to enjoy the benefits of both static typing and dynamic dispatch, which is enum. Rust's enum is an ADT (Algebraic Data Type), also known as tagged union, and it can represent our operators very conveniently:
pub enum Operator {
Get {
table: String,
},
Select {
child: Box<Self>,
predicate: String,
},
Project {
child: Box<Self>,
projects: String,
},
}
fn plan() -> Operator {
// select a from t where a = 1;
Operator::Project {
child: Box::new(Operator::Select {
child: Box::new(Operator::Get {
table: "t".to_string(),
}),
predicate: "a = 1".to_string(),
}),
project: "a".to_string(),
}
}With this, we can freely represent operator trees of various shapes, and the design of the IR begins to get on the right track.
Scalar expression
Although we have introduced the operators Select and Project, the Select Predicate and Project Expression still exist in the form of strings, which cannot meet the requirements for analysis and optimization. Therefore, we need to design an IR for these expressions as well.
Looking back, after being processed by the Parser, SQL strings are transformed into AST, and the expressions within them become Expr nodes, roughly like this:
pub enum Expr {
ColumnRef(ColumnRef),
Literal(Literal),
Function(Function),
BinaryOp(BinaryOp),
UnaryOp(UnaryOp),
Subquery(SelectStmt),
}The expression itself is a recursive structure, and the Expr node of AST is also a recursive structure. Can we lazily use the Expr node directly as part of our SQL IR? Let's give it a try first.
After replacing string with Expr, we can obtain:
pub enum Operator {
Get {
table: String,
},
Select {
child: Box<Self>,
predicate: Expr,
},
Project {
child: Box<Self>,
projects: Vec<Expr>,
},
}Next, let's try some common analysis using the given SQL statement to see if it works well:
select a from t
where exists (select * from t1 where t.a = t1.a)- Q: Which tables and columns does
ExprinProjectdepend on? A: It uses a column calleda, but I don't know which table it belongs to, maybe this column doesn't even exist. - Q: What is the return type of
ExprinProject? A: I don't know, there is no type information included inExpr. - Q: Is the subquery in
Selecta correlated subquery? A: I don't know, the subquery inExpris just an unprocessed AST.
Ok, it seems that Expr is not as useful as we imagined. In order to conduct the above analysis, we need to design a more informative IR. To distinguish it from Expr, we will name it ScalarExpr.
Summarizing the above analysis, our requirements for ScalarExpr are as follows:
- All identifiers must be resolved to fully qualified names.
- Type information needs to be injected and undergo type check.
- All subqueries need to be transformed into SQL IR form.
Combining the above requirements, along with some desugar, ScalarExpr would look something like this:
pub enum ScalarExpr {
ColumnRef(Vec<Identifier>, Type),
Literal(Value, Type),
Function(Signature, Vec<Self>),
Subquery(Quantifier, Box<Operator>),
}In this way, the design of the expression's IR is also formed. Let's integrate the entire set of SQL IR together.
The IR
After the above design, we have:
Operator, a tree structure capable of flexibly expressing various SQL queries.ScalarExpr, providing rich semantic information.
Although some key operators are still missing, such as Join, Union, Aggregate, etc. However, since the overall framework is already very clear, we can follow the same pattern and add them as well.
After integration, we have a fairly perfect SQL IR.
pub enum ScalarExpr {
ColumnRef(Vec<Identifier>, Type),
Literal(Value, Type),
Function(Signature, Vec<Self>),
Subquery(Quantifier, Box<Operator>),
}
pub enum Operator {
Get {
table: String,
},
Select {
child: Box<Self>,
predicate: ScalarExpr,
},
Project {
child: Box<Self>,
projects: Vec<ScalarExpr>,
},
Join {
kind: JoinKind,
condition: ScalarExpr,
left: Box<Self>,
right: Box<Self>,
},
UnionAll {
left: Box<Self>,
right: Box<Self>,
},
Aggregate {
group_by: Vec<ScalarExpr>,
aggr_exprs: Vec<ScalarExpr>,
child: Box<Self>,
},
}Because it is too perfect, I have decided to give this IR an imposing name - The IR.
Property Derivation
When we want to analyze and optimize IR, we always need to obtain some properties of the IR. We can calculate these properties by writing an analyzer that traverses the entire IR, but this requires a lot of effort to maintain the state of the context in which the IR is located.
Fortunately, SQL as a declarative query language for data flow is quite simple, and we can use its features to calculate properties.
The data flow and parent-child relationships between operators in The IR are closely related and presented as a DAG (directed acyclic graph), where all data flows from child nodes to parent nodes.
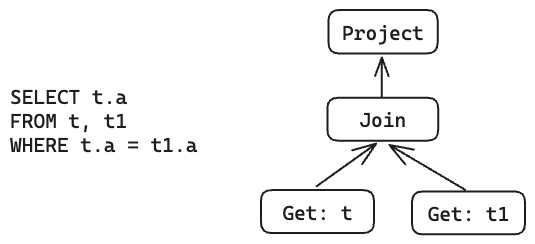
Under this characteristic, it is simple to compute the property of a certain IR node. It only requires recursively computing the property of each child node and then calculating its own property based on these properties. We refer to this process as property derivation.
pub struct Property;
fn derive_property(op: &Operator) -> Property {
// Calculate the properties of the children operators.
let children_property: Vec<Property> = op
.children()
.map(derive_property)
.collect();
// Calculate property with the children properties.
op.calculate_property(&children_property)
}In SQL optimization, commonly used properties can be divided into two categories: relational/logical properties that describe the characteristics of a data set and physical properties that describe the physical characteristics of the data.
Common relational properties include:
- Information about the
attributes/columnscontained in the dataset Cardinalityof the dataset, indicating the number of records in the datasetStatistics, representing the data distribution of attributesConstraints, representing constraints on attributes, such asNOT NULLFunctional dependency, indicating the functional dependency relationship between attributes
Common physical properties include:
- Order
- Degree of parallelism (DOP)
- Data distribution
- Data partition
Combining the properties of relational algebra, we can describe the differences between types of properties.
Assuming there are relations R and S: the relational property of R is RP_R, and the physical property is PP_R; the relational property of S is RP_S, and the physical property is PP_S.
We can obtain:
It is not difficult to see that the equivalence relationship between two relations can determine the equivalence relationship of relational properties, but the equivalence relationship of physical properties is not affected by the equivalence relationship of relations.
The content about combining properties with specific query optimization algorithms will be discussed in detail in subsequent articles.
With property derivation, we can use theorems from relational algebra to optimize The IR while ensuring correctness.
So the next question is, what should the property look like?
Relational properties
The most important part of relational property is the representation of attributes. In naive relational algebra, each relation is composed of sets of tuples, and each attribute in a tuple has its own unique name. It is natural for us to directly consider using the tuple schema as the representation of attributes.
Let's first recall how a table is created.
create table t(a int);In SQL, we use DDL (Data Definition Language) to create and manage various tables. When creating a table, we need to specify its table schema, which includes the specific definition of each column in the table, corresponding to attributes in relational algebra. The structure of the table schema might look something like this:
pub struct TableSchema {
pub name: String,
pub columns: Vec<ColumnDefinition>
}
pub struct ColumnDefinition {
pub name: String,
pub column_type: Type,
pub not_null: bool,
}Since ColumnDefinition and attribute have a one-to-one correspondence, can we directly use ColumnDefinition to represent the property of attribute?
We can try adding support for attributes in The IR first.
fn derive_attributes(op: &Operator) -> Vec<ColumnDefinition> {
// Calculate the attributes of the children operators.
let children_attributes: Vec<Vec<ColumnDefinition>> =
op.children().iter().map(derive_attributes).collect();
// Calculate attributes with the children attributes.
op.calculate_attributes(&children_attributes)
}First, we need to make some modifications to The IR and add table schema information for the Get operator.
pub enum Operator {
Get {
table: String,
schema: Vec<ColumnDefinition>,
},
// Nothing changed for other variants
}Then we implement attribute derivation for the Operator.
impl Operator {
fn calculate_attributes(&self, children: &[Vec<ColumnDefinition>]) -> Vec<ColumnDefinition> {
match self {
Operator::Get { schema, .. } => {
let attributes = schema.clone();
attributes
}
Operator::Select { .. } => children[0].clone(),
Operator::Join { .. } => {
let mut attributes = children[0].clone();
attributes.extend(children[1].clone());
attributes
}
Operator::UnionAll { .. } => children[0].clone(),
Operator::Project { .. } => todo!(),
Operator::Aggregate { .. } => todo!(),
}
}
}Most of the operator implementations went smoothly, but it can be seen that Project and Aggregate have been marked as todo. At this point, we will find that Project and Aggregate cannot directly generate their own attributes using children attributes.
Going back to relational algebra, the purpose of Project is to trim the shape of tuples or modify the name of attributes. This kind of SQL expression like SELECT a + 1 AS b FROM t cannot be expressed as a naive Project; as for Aggregate, it is not even present in basic relational algebra, it is an extension to relational algebra.
The theory of relational algebra no longer exists!
However, despite this, the project still needs to continue. We need to introduce some village rules to expand the definition of relational algebra. Here we provide the formal definitions of Project and Aggregate in The IR.
Project represents the attributes in relationship R as input, output a tuple consisting of n function mappings f_1 to f_n.
Aggregate represents grouping the tuples in relationship R according to m attributes k_1 to k_m, and applying n function mappings f_1 to f_n on each group, finally outputting the grouped tuples.
The biggest change in this village rule is the introduction of derived columns. For columns directly from tables in SQL, we call them base table columns; for columns calculated through Project/Aggregate, we call them derived columns.
Before introducing the concept of derived columns, we could ensure that all data sources would ultimately point to the Get operator. However, after its introduction, this convention was broken and a concept similar to scope in programming languages emerged. We need to be more careful when optimizing.
After having village rule, we can also achieve attribute derivation for Project and Aggregate. However, at the same time, we also need to make some modifications to the structure of The IR.
pub enum Operator {
Project {
child: Box<Self>,
projects: Vec<(ScalarExpr, String)>,
},
// Others
}
impl Operator {
fn calculate_attributes(&self, children: &[Vec<ColumnDefinition>]) -> Vec<ColumnDefinition> {
match self {
Operator::Project { projects, .. } => {
let attributes: Vec<ColumnDefinition> = projects
.iter()
.map(|(expr, alias)| ColumnDefinition {
name: alias.clone(),
column_type: expr.column_type(),
not_null: expr.nullable(),
})
.collect();
attributes
}
Operator::Aggregate {
group_by,
aggr_exprs,
..
} => {
let mut attributes: Vec<ColumnDefinition> = group_by
.iter()
.map(|expr| ColumnDefinition {
name: expr.name(),
column_type: expr.column_type(),
not_null: expr.nullable(),
})
.collect();
attributes.extend(aggr_exprs.iter().map(|expr| ColumnDefinition {
name: expr.name(),
column_type: expr.column_type(),
not_null: expr.nullable(),
}));
attributes
}
// Others
}
}
}In this way, we can calculate the attributes property for all operators. Come and try it out!
First, let's take a look at the most common and effective optimization in SQL - predicate pushdown. This optimization can reduce the computational workload of other operators by pushing down the Select operator into other operators, while ensuring that the overall query result remains unchanged. It is very concise and elegant.
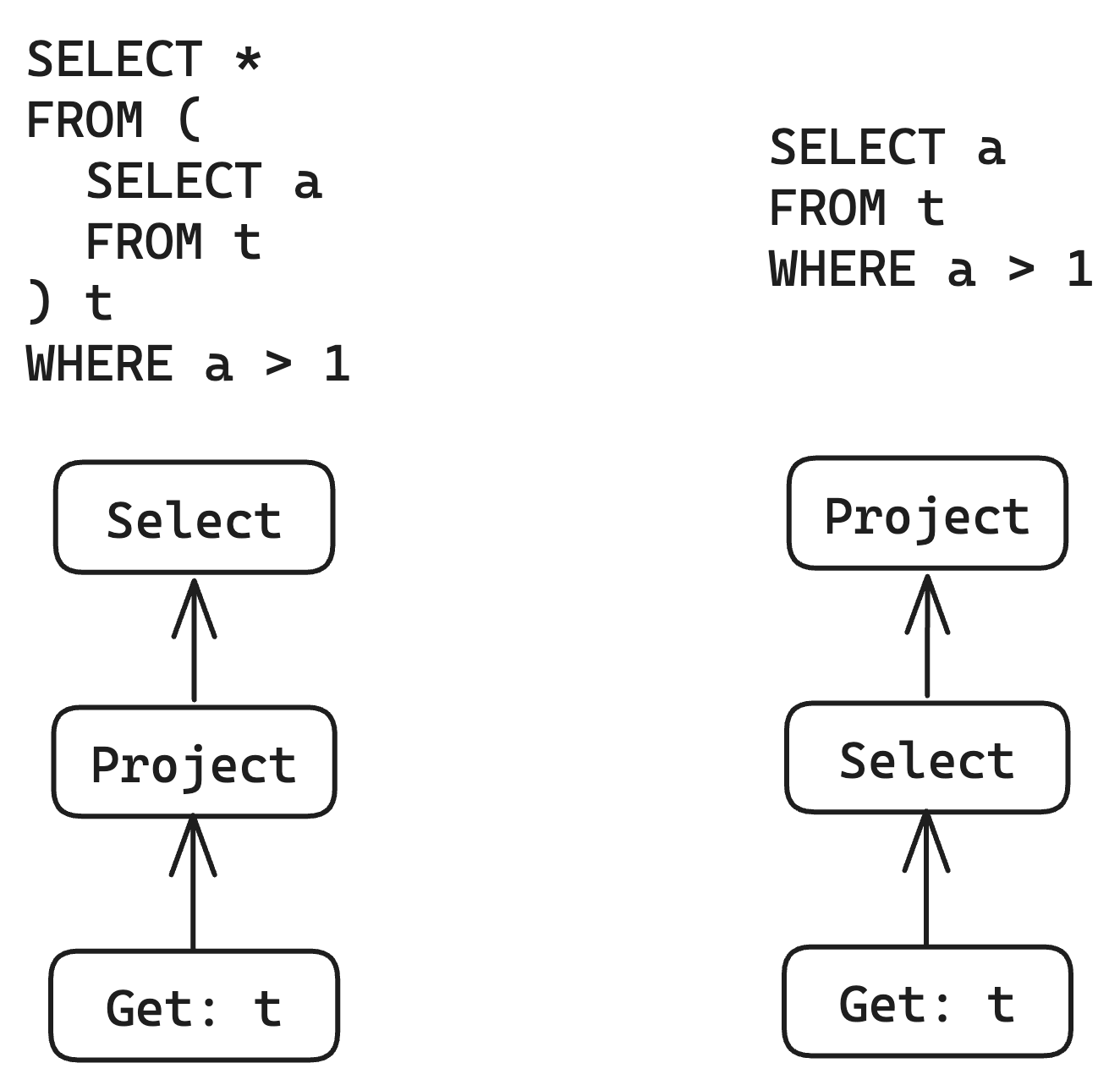
Let's try to implement this optimization on The IR. The idea is very simple, just swap the positions of Select and Project based on the relational algebra theorem. However, since we introduced derived columns, we must check if the predicate in Select depends on the column generated by Project.
fn push_down_select_project(op: &Operator) -> Option<Operator> {
match op {
Operator::Select {
child: project @ box Operator::Project { child, projects },
predicate,
} => {
let project_attributes: Vec<ColumnDefinition> = derive_attributes(&project);
let predicate_used_columns: Vec<String> = predicate.used_columns();
// Check if the predicate uses any column from the project.
let used_derived_columns = predicate_used_columns.iter().any(|used_column| {
project_attributes
.iter()
.any(|attr| attr.name == *used_column)
});
if used_derived_columns {
None
} else {
Some(Operator::Project {
child: Box::new(Operator::Select {
child: child.clone(),
predicate: predicate.clone(),
}),
projects: projects.clone(),
})
}
}
_ => None,
}
}It seems to be basically usable now, which is delightful. Let's try a more complex example, such as trying SQL with Join:
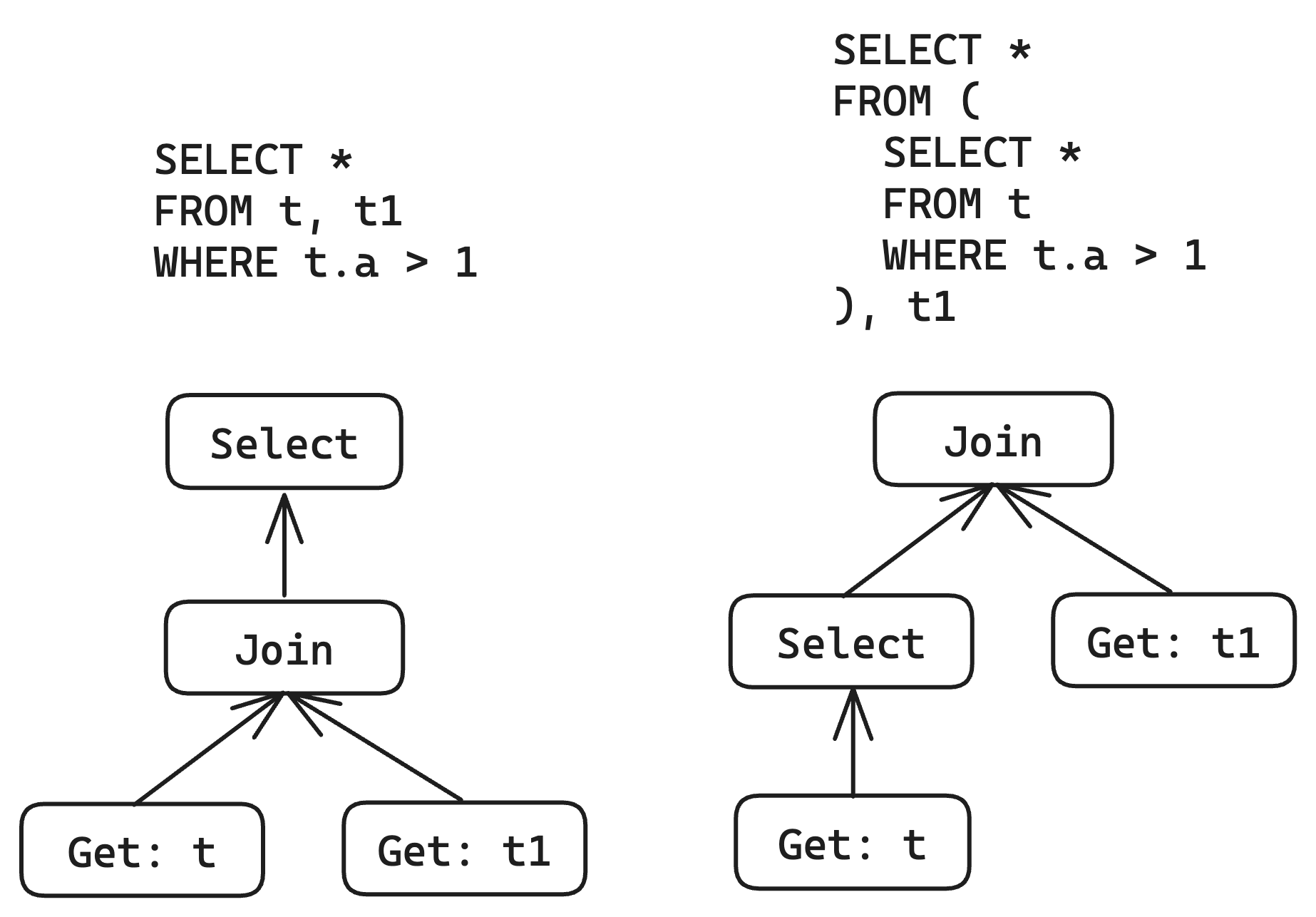
Because Join does not generate additional derived columns like Project, the logic for checking will be relatively simpler. Let's first implement an optimization that attempts to push Select down to the left child of Join:
fn push_down_select_join_left(op: &Operator) -> Option<Operator> {
match op {
Operator::Select {
child: join @ box Operator::Join { left, right, .. },
predicate,
} => {
let left_attributes: Vec<ColumnDefinition> = derive_attributes(&left);
let predicate_used_columns: Vec<String> = predicate.used_columns();
// Check if the predicate only uses column from left.
let only_left = predicate_used_columns
.iter()
.all(|used_column| left_attributes.iter().any(|attr| attr.name == *used_column));
if only_left {
Some(Operator::Join {
left: Box::new(Operator::Select {
child: left.clone(),
predicate: predicate.clone(),
}),
right: right.clone(),
..join.clone()
})
} else {
None
}
}
_ => None,
}
}Everything looks great, but the devil often hides in the details. Let's take a look at the output of this example in PostgreSQL:
leiysky=# create table t(a int);
CREATE TABLE
leiysky=# create table t1(a int);
CREATE TABLE
leiysky=# insert into t values(1);
INSERT 0 1
leiysky=# insert into t1 values(1);
INSERT 0 1
leiysky=# select * from t, t1 where t.a = 1;
a | a
---+---
1 | 1
(1 row)The final result returned has two attributes called a. In the current implementation of The IR, we cannot know which side this Select should be pushed down to. Because when we check which side the predicate that depends on a can be pushed down to, we will find that both sides of the Join can satisfy it. Although it is not allowed to have multiple columns with the same name in the same table, there is no such restriction between different tables.
As the open-source database product with the highest support for ANSI SQL, PostgreSQL naturally handles this kind of problem very well. Through the EXPLAIN statement, we can see that it pushes down the Select to the correct place.
leiysky=# explain(verbose) select * from t, t1 where t.a = 1;
QUERY PLAN
----------------------------------------------------------------------
Nested Loop (cost=0.00..491.78 rows=33150 width=8)
Output: t.a, t1.a
-> Seq Scan on public.t1 (cost=0.00..35.50 rows=2550 width=4)
Output: t1.a
-> Materialize (cost=0.00..41.94 rows=13 width=4)
Output: t.a
-> Seq Scan on public.t (cost=0.00..41.88 rows=13 width=4)
Output: t.a
Filter: (t.a = 1)
(9 rows)As a perfect SQL IR, The IR must also have its own solution. If we carefully observe this query, we will find that the predicate of Select is represented by a qualified name. If an unqualified name is used, PostgreSQL will throw such an error:
leiysky=# select * from t, t1 where a = 1;
ERROR: column reference "a" is ambiguous
LINE 1: select * from t, t1 where a = 1;Because in the current context, a is ambiguous, but t.a is not. Let's try using qualified name to represent attribute property to solve this problem. For this purpose, we need to make some code changes.
pub struct QualifiedName(pub Vec<String>);
impl QualifiedName {
/// If the current name can be used to refer another name
pub fn can_refer(&self, other: &Self) -> bool {
self.0.len() <= other.0.len()
&& self.0.iter().zip(other.0.iter()).all(|(a, b)| a == b)
}
}
pub struct ColumnDefinition {
/// Use qualified name
pub name: QualifiedName,
pub column_type: Type,
pub not_null: bool,
}
fn resolve_attribute(
attributes: &[ColumnDefinition],
name: &QualifiedName,
) -> Option<ColumnDefinition> {
let candidates: Vec<ColumnDefinition> = attributes
.iter()
.filter(|attr| attr.name.can_refer(name))
.collect();
if candidates.len() == 1 {
Some(candidates[0].clone())
} else if candidates.len() > 1 {
panic!("Watch out, ambiguous reference found!")
}else {
None
}
}
fn push_down_select_join_left(op: &Operator) -> Option<Operator> {
match op {
Operator::Select {
child: join @ box Operator::Join { left, right, .. },
predicate,
} => {
let left_attributes: Vec<ColumnDefinition> = derive_attributes(&left);
let predicate_used_columns: Vec<QualifiedName> = predicate.used_columns();
// Check if the predicate only uses column from left.
let only_left = predicate_used_columns
.iter()
.all(|used_column| resolve_attribute(&left_attributes, used_column).is_some());
if only_left {
Some(Operator::Join {
left: Box::new(Operator::Select {
child: left.clone(),
predicate: predicate.clone(),
}),
right: right.clone(),
..join.clone()
})
} else {
None
}
}
_ => None,
}
}In this way, the above problem is solved, and we have the ability to handle complex attribute references. However, there is still a long way to go before achieving a perfect solution. Let's take another example:
leiysky=# select * from (select * from t1) as t, t1 where t.a = 1;
a | a
---+---
1 | 1
(1 row)Although SQL does not allow the use of multiple identical table names in the same FROM clause, we can bypass this by using an inlined view or CTE. According to our current implementation, when processing t.a = 1, we have two t1.a attributes instead of t.a because we did not handle the alias of the inlined view. Therefore, we need to add a Project specifically for renaming attributes.
So the problem arises again, because we only renamed some columns and treated them as derived columns, which added a lot of burden to our Select pushdown. Therefore, we must modify the definition of The IR and various related codes to serve the mapping of names.
pub enum Operator {
Project {
child: Box<Self>,
// (Expression, Source name, Alias)
projects: Vec<(ScalarExpr, QualifiedName, QualifiedName)>,
},
// Others
}These problems can be solved by writing a little more code, but take a look at the next example. I believe that most people will go crazy just like me:
leiysky=# select a from t natural join t1;
a
---
1
(1 row)
leiysky=# select t.a from t natural join t1;
a
---
1
(1 row)
leiysky=# select t1.a from t natural join t1;
a
---
1
(1 row)
leiysky=# select * from t natural join t1;
a
---
1
(1 row)
leiysky=# select a from t join t1 on t.a = t1.a;
ERROR: column reference "a" is ambiguous
LINE 1: select a from t join t1 on t.a = t1.a;Of course, we can add all kinds of strange restrictions to the code, create difficult-to-maintain loopholes to maintain this property, and ensure the correctness of these properties while optimizing. But for lazy programmers, finding a simpler design is a better choice.
Welcome to the Deep Water Zone.
The IR made simple
The initial version of The IR was very concise and elegant, but in order to achieve more functionality and support more complex requirements, we added a lot of information that we don't want to focus on.
In general, the ideal state of The IR should be:
- Having a concise algebraic structure
- Operator nodes being completely independent from each other
- Not having to deal with names (only for debugging and display purposes)
Let's take a moment to reflect, does IR really rely on name? We initially used name to represent attributes mainly based on intuition and reused the table schema. However, there is a lot of useless information embedded in the name, which is of no help to our optimization. It's similar to various symbol names in programming languages that eventually become memory addresses and register numbers during program execution.
Without a name, attributes cannot be distinguished. Is a name really such an inconvenient thing?

NOTE: the above image means "Is a name really such an inconvenient thing?"
Ultimately, what we need is to assign a unique id to each attribute, whether it is an integer or a string. Our sole purpose is to differentiate and reference attributes using these ids. All name resolution will be handled in AST lowering; I only want the attribute id!
After the redesign, we have changed the way attributes are represented and also made some changes to The IR's definition. By default, we use int64 as the attribute id type.
pub type Id = i64;
pub struct Attribute {
pub id: Id,
pub column_type: Type,
pub nullable: Type,
}
pub enum ScalarExpr {
ColumnRef(Id),
// Others
}The design of the id generally cannot be separated from the corresponding context. In SQL IR, the common design methods for attribute id can mainly be divided into two categories:
- One is based on the abstraction of tuple attribute that we have used before, using the index of attribute in tuple as its id. We call this kind of id as
local id. The characteristic of this design is that the id of the same logical attribute will change with different operators it belongs to. The advantage of this design is that it can be inferred from the operator tree without relying on external states for maintenance. However, a disadvantage is that frequent remapping of ids is required when converting operators. - Another method is to maintain a global id generator and assign a unique id to all attributes in SQL IR. We call this kind of id as
global id. The advantage of this design is that it decouples attributes from tuple schema and allows representation using an unordered collection structure likeHashMap<Id, Attribute>. It also helps property derivation through set operations and reduces maintenance complexity. However, a disadvantage is that operator trees using global ids depend on external states and cannot exist independently.
The use of these two different designs will have a significant impact on the specific implementation of the optimizer.
For example, regarding this optimization:
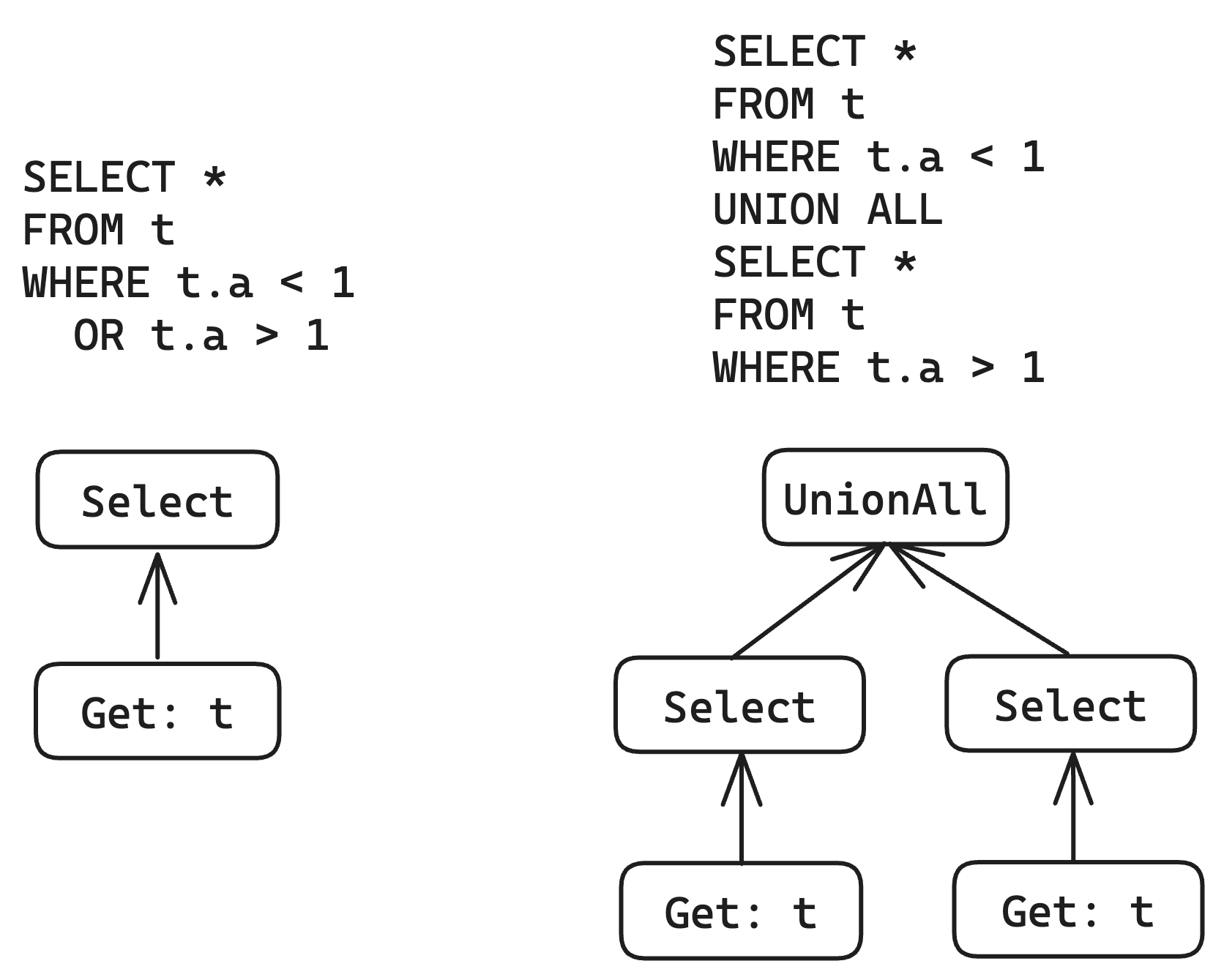
When there are suitable indexes available, this optimization can avoid full table scans and improve performance.
If using the local id design, implementing this optimization is very simple, just need to copy the entire operator tree and finally connect them with UnionAll.
But if using the global id design, this is a non-trivial operation, even can be said to be very painful. In order to distinguish different attributes, we must generate new IDs for all attributes while copying the operator tree at the same time, and then replace all places that reference these attributes with new IDs. This will cause many troubles when the query is more complex.
For example, when optimizing join order:
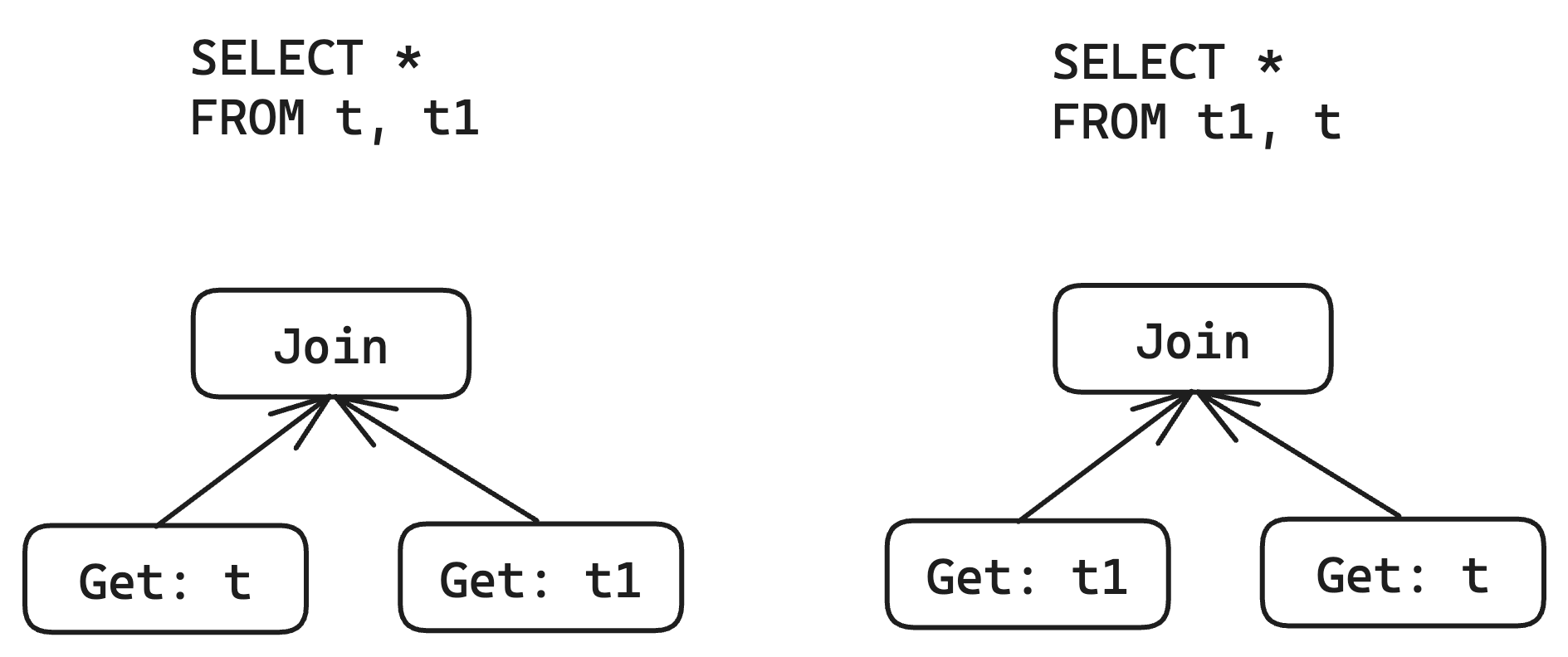
According to the commutative law of Join operators, we can legally exchange the left and right child of a Join.
When using global id design, because attributes can be represented as an unordered set, this operation has no impact on property derivation.
However, when using local id design, this operation becomes extremely painful.
Apart from optimization-related parts, there are also significant differences in representing correlated subqueries. Correlated subquery is a special type of subquery that can access attributes outside its own scope. We refer to accessing such special attributes as outer reference.

Many programming languages also support similar operations, which allow accessing variables that are not defined within the function by binding them to a specific environment. This special type of function is called a closure.
fn main() {
let a = 1;
let f = || {
let b = a; // a is captured from outside
println!("{}", b);
}; // f is a closure
f(); // stdout: 1
}The design using global id can determine whether the subquery is correlated through attribute property calculation. However, when using local id design, we generally need to maintain an additional scope id in the ColumnRef of scalar expression, which is very cumbersome to implement.
Correlated subquery is a very big topic, and we may discuss it in subsequent articles.
It can be seen that both designs have their own advantages and disadvantages. In engineering practice, we need to choose a suitable design based on our own needs. Personally, I think global id is a better design because it can easily solve problems in most cases.
After the transformation using global id, the code of The IR can be greatly simplified.
pub type Id = i64;
pub struct Context {
pub id_gen: Id,
}
pub struct Attribute {
pub id: Id,
pub column_type: Type,
pub nullable: Type,
}
pub type AttributeSet = HashMap<Id, Attribute>;
pub enum ScalarExpr {
ColumnRef(Id),
Literal(Value, Type),
Function(Signature, Vec<Self>),
Subquery(Quantifier, Box<Operator>),
}
pub enum Operator {
Get {
table: String,
output_columns: AttributeSet,
},
Select {
child: Box<Self>,
predicate: ScalarExpr,
},
Project {
child: Box<Self>,
projects: Vec<(ScalarExpr, Id)>,
},
Join {
kind: JoinKind,
condition: ScalarExpr,
left: Box<Self>,
right: Box<Self>,
},
UnionAll {
left: Box<Self>,
right: Box<Self>,
},
Aggregate {
group_by: Vec<ScalarExpr>,
aggr_exprs: Vec<(ScalarExpr, Id)>,
child: Box<Self>,
},
}After transferring the complexity to the AST lowerer, we can confidently say that The IR is now a production-ready SQL IR. It supports all SQL operations and common optimizations, has a user-friendly API, and is also very easy to understand.
What's more important is that no one understands The IR better than the readers of this article, and any reader can easily extend The IR according to their own needs.
Afterword
Finally, we have reached the end of this article.
As the opening of the series, in this article I simply discussed some focal points in SQL IR design without delving into the details of various algorithms.
However, sharing the design process of IR is an interesting thing. Understanding multiple IRs is like understanding why a roadside tree grows crooked. To someone seeing it for the first time, the tree's unusual shape is puzzling. However, locals who have lived around it are aware of its backstory: when it was young, the tree became bent due to the habit of hanging preserved meat on its branches.
This little thing is an important reason for the final result, but it is too insignificant to be voluntarily shared by those who know - of course, in reality, no one often cares about the reasons behind it either.
Database development is a niche field with many engineering practices and experiences. These experiences are rarely circulated among people and I don't want them to disappear with changing times like America's moon landing technology; hence my original intention to write this series of articles came about.
In the next article, I will share related content about optimizer architecture; please stay tuned.